Variance and Bankroll Management
每个扑克玩家都必须具备的重要软技能
尽管我们尽了最大努力来最大限度地提高在牌桌上的优势,但扑克的核心是博弈游戏。 它是可以打败的,但它仍然是围绕与其他博弈游戏相同的基础支柱构建的:疯狂、令人痛苦、令人麻木的变化!
扑克到底是运气还是技巧?
两者皆有! 运气或技巧的多少取决于你玩了多少手牌。 从长远来看,微小的边缘会被放大。 从短期来看,你的结果主要取决于运气。 但在足够长的时间内,即使是很小的优势也是不可避免的。 从短期来看,你的结果主要取决于运气,而从长远来看,则取决于技巧!
到底什么是方差?
术语方差是指数据集中数字之间的差异的统计测量。 在扑克中,方差是指你的结果有多么“不稳定”!
在方差较高的游戏中,玩家的结果可能会进一步偏离给定样本的预期。
方差和资金管理
方差通过“标准偏差”指标来衡量。 您可以在大多数扑克 HUD 中找到此指标,但也可以直接根据结果计算。 对于现金游戏,以 BB/100 来衡量。
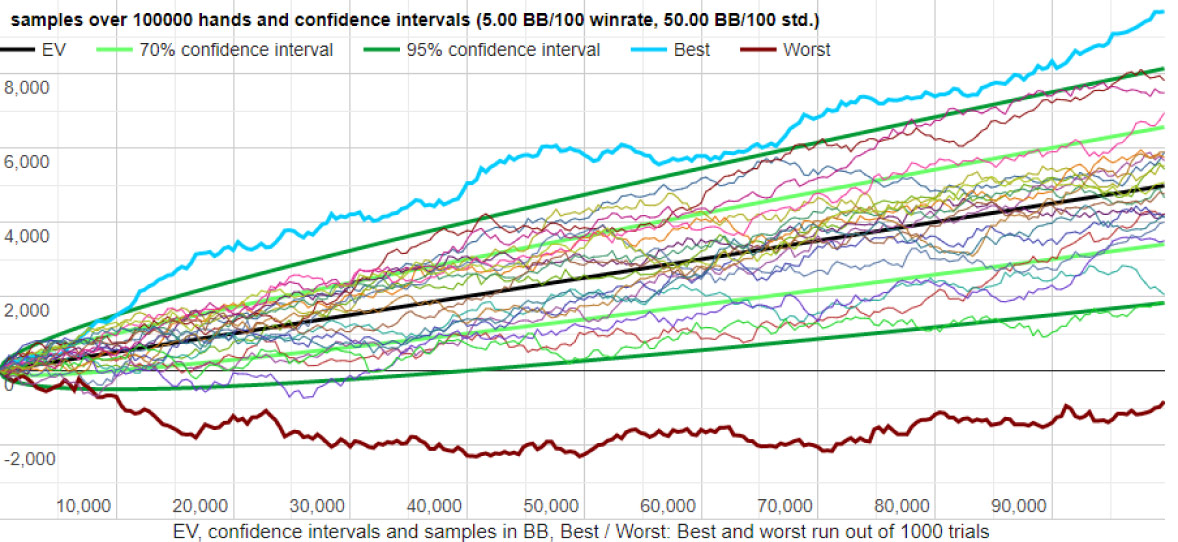
我们来看一些例子。 下图是给定一组输入的 20 次随机运行的示例(来源:Primedope)
方差比较低的结果
请注意,最佳和最差的运行范围在 -1,000 BB 和 +10,000 BB 之间。
方差比较高的结果
请注意,最佳和最差的运行范围在 -17,000 BB 和 +22,000 BB 之间。
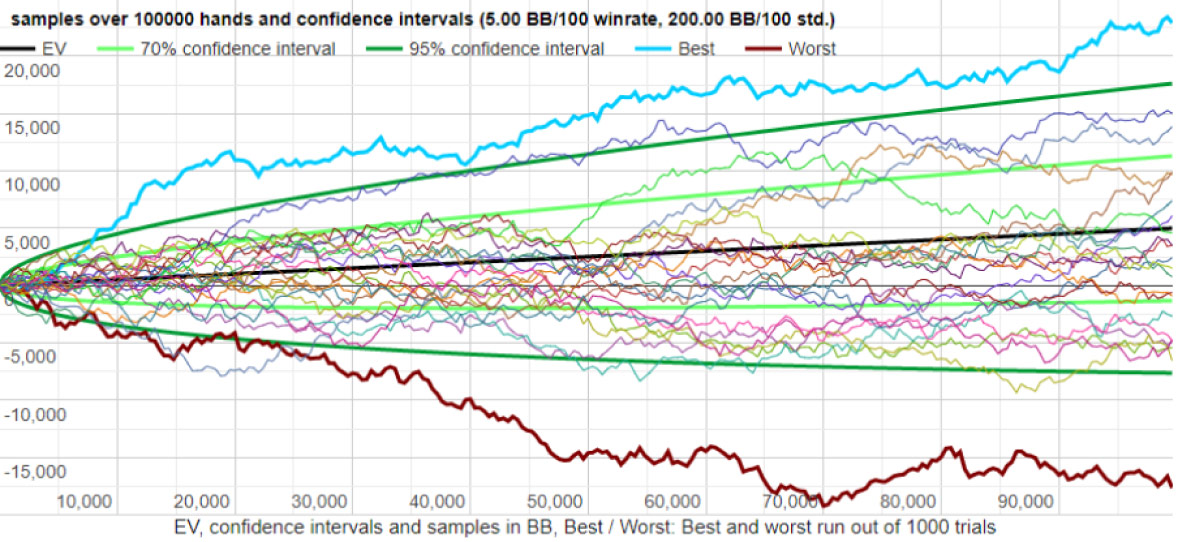
两名玩家的胜率相同,但方差较高的玩家的最佳成绩和最差成绩之间的差距要大得多!
大数法则
赌徒谬误在扑克玩家中非常普遍。 假设我们抛一枚均匀的硬币,连续 6 次正面朝上。 下一次抛硬币正面朝上的概率是多少?
如果你迷信,你可能会认为你“欠”尾巴。 但现实根本不是这样的。 下一次翻转是 50%/50%。 你第七次掷出正面的可能性与第一次掷出正面的可能性一样。
方差和资金管理
硬币抛数千次后,预计正面和反面会趋于平衡。 但这并不是因为某种外力,这就是大数法则。 想象一下,我们抛掷 1000 次,正面保持 6 次抛掷领先。 至此,我们已经翻转了 503 个正面和 497 个反面 —— 实际上只是领先6个点的预期值而已。 此时,正面为50.3%,反面为49.7%。
我们抛10万次并保持同样的6次差异。 现在是 50.0003% 正面和 49.9997% 反面。 尽管尾巴并未消除,但所谓的“运气”似乎趋于平衡。 这就是大数法则。
因此,仅仅因为你运气差一点并不意味着你倒霉。 老天不欠你什么。 每手牌都是独立的,不存在记忆。
反之亦然。 你跑得好也不意味着运气补偿给你。 事实是,扑克中的方差远远超出了人类能够真正概念化的程度。 如果您曾经使用过扑克方差计算器,您会发现需要数万手牌才能看到统计上显着的优势实现。
置信区间
我们最常见的问题之一是“我需要多少手牌才能确定我的胜率?”。 这个问题的问题是它没有真正的答案。 在数学中,我们使用置信区间来解决这些未知因素!
置信区间遵循68-95-99规则:
68% 的情况下,您的结果会落在平均值的 1 个标准差 σ 内
95% 的总体处于平均值的 2 个标准差 (2σ) 之内
99.7% 的总体处于平均值的 3 个标准差 (3σ) 之内
方差分布
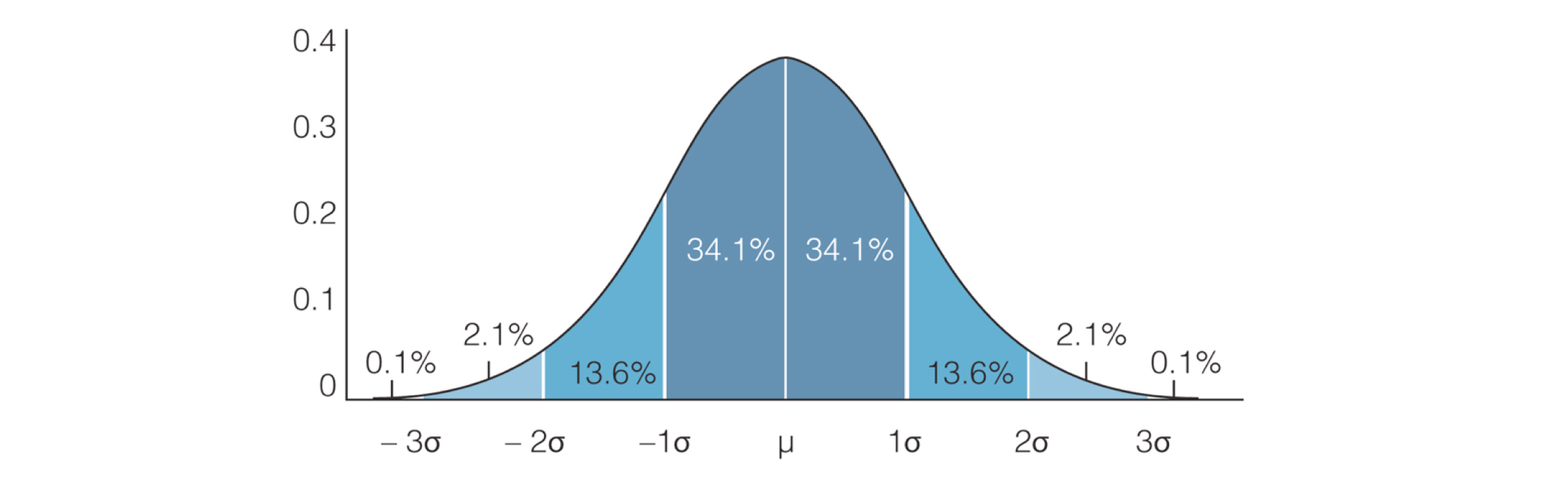
μ = Expected Value
-1σ to 1σ = 1 Standard Deviation (ie: ~2/3 of the time, your results will fall within this range)
-2σ to 2σ = 2 Standard Deviation (ie: 95% of the time, your results will fall within this range)
-3σ to 3σ = 3 Standard Deviation (ie: 99.7% of the time, your results will fall within this range)
看个例子


假设您的“真实”(平均)胜率为 2.5 BB/100。 这是你的预期价值。
10 万手牌后的标准差 (σ) 为 3.16 BB/100。
更好描述胜率的方法是:
2.5 ± 3.16 BB/100. (Winrate ± σ)
换句话说:
- 70% 的时间 (~1σ) 您的结果将落在 -0.66 BB/100 和 5.66 BB/100 之间
- 95% 的时间 (2σ) 您的结果将落在 -3.82 和 8.82 BB/100 之间
在科学中,未知变量被分配误差幅度和置信区间,而不是确切的数字。 您的胜率是一个未知变量。 因此,不可能给出一个准确的数字。 您能做的最好的事情就是分配一些误差范围。
误差幅度的公式是标准差和交易量的函数。 投入更多的数量或降低方差,将降低误差幅度并增加结果的可信度。 公式如下:
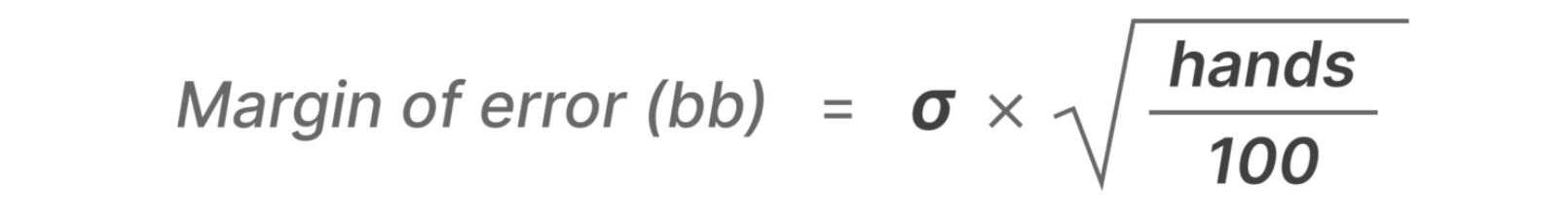
其中 σ 是以 BB/100 为单位的标准差,手数就是您玩过的手数。 例如,上面我们看到标准差为 100 BB/100,玩了 100k 手牌。 100 * (100,000/100)^0.5 = 3162。换句话说,结果是正负3162 BB,即3.16 BB/100。 上图中显示为“100000手后的标准差”,但更容易将其视为误差幅度。
管理风险
方差可以通过免费计算机程序基于上述输入来计算。
为此目的推荐的一些网站是 Primedope 和 ReviewPokerRooms。 了解方差的界限是将结果和期望置于背景中的好方法。 花一些时间自己尝试不同的输入并查看结果输出是非常宝贵的。
上述工具适用于现金游戏。 MTT 玩家往往会体验到更大的差异。 试试这个 MTT 方差计算器!
资金管理指南
本文的目的是为您提供建立自己的资金管理策略的工具,而不是提供一些答案。 您的 BRM 取决于您的风险状况。 然而,我们根据常识概述了以下一些非常基本的 BRM 指南:
对于现金玩家: 35 至 65 买入
- 切勿冒超过 5% 的风险
对于锦标赛玩家:75 至 125 个买入
- 切勿冒超过 2% 的风险
凯利准则
凯利准则告诉您应该用您的资金的哪一部分来冒险。 它会考虑您的投注优势和赔率,并输出您应该承担多少资金风险。
资金管理策略的核心是最大化您的优势而不过度发挥您的资金。 这就是凯利所做的。
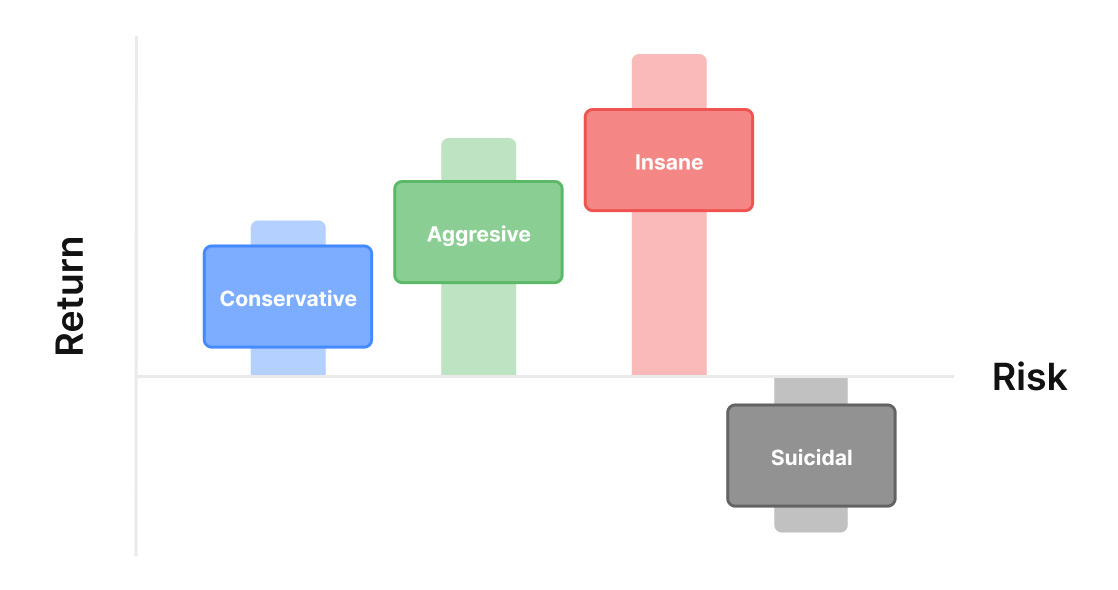
凯利准则的公式概述如下:
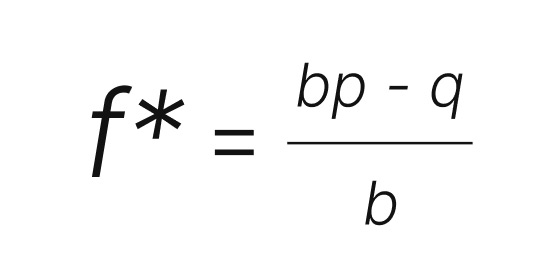

来尝试一个例子
你玩 HU SnG,平均投资回报率 (ROI) 为 5%。
您的资金为 1000。
您应该玩什么赌注才能尽快增加您的资金?
A) 100 买入
B) 50 买入
C) 25 买入
D) 10 买入
答案
B) 50 美元买入
凯利准则的基本前提是你应该冒你的优势的风险! 对于简单的 1:1 投注,如果您有 5% 的优势,您应该拿 5% 的资金冒险,在本例中为 50 美元。
以下是如何用数学来解决这个问题:
b = 1
p = 52.5%
q = 47.5%
f* = p – q = ROI
f* = 5%
5% of $1000 = $50
这是基于“全凯利”策略。 完整的凯利策略就像红线你的引擎! 在实践中,实施半凯利甚至四分之一凯利策略通常会更好。 half-kelly 策略捕获了 75% 的增长,但仅承担 25% 的方差。 所以 C) 25 美元 BI 在实践中可能是更好的答案。
最佳资金管理策略
凯利准则告诉您应该用您的资金的哪一部分来冒险。 您应该冒多大的风险取决于您的胜率和方差。 请记住,凯利是边界,而不是目标! 在实践中你的投资应该少于凯利。
我们可以使用数学将现金游戏或其他格式的扑克胜率转化为最佳 BRM 策略。 我们构建了一个方便的 BRM 优化工具来帮助您更快地升级!
该计算器可以找到证明增加赌注和承担更多方差以换取更高每小时获胜率的合理性所需的最低资金。
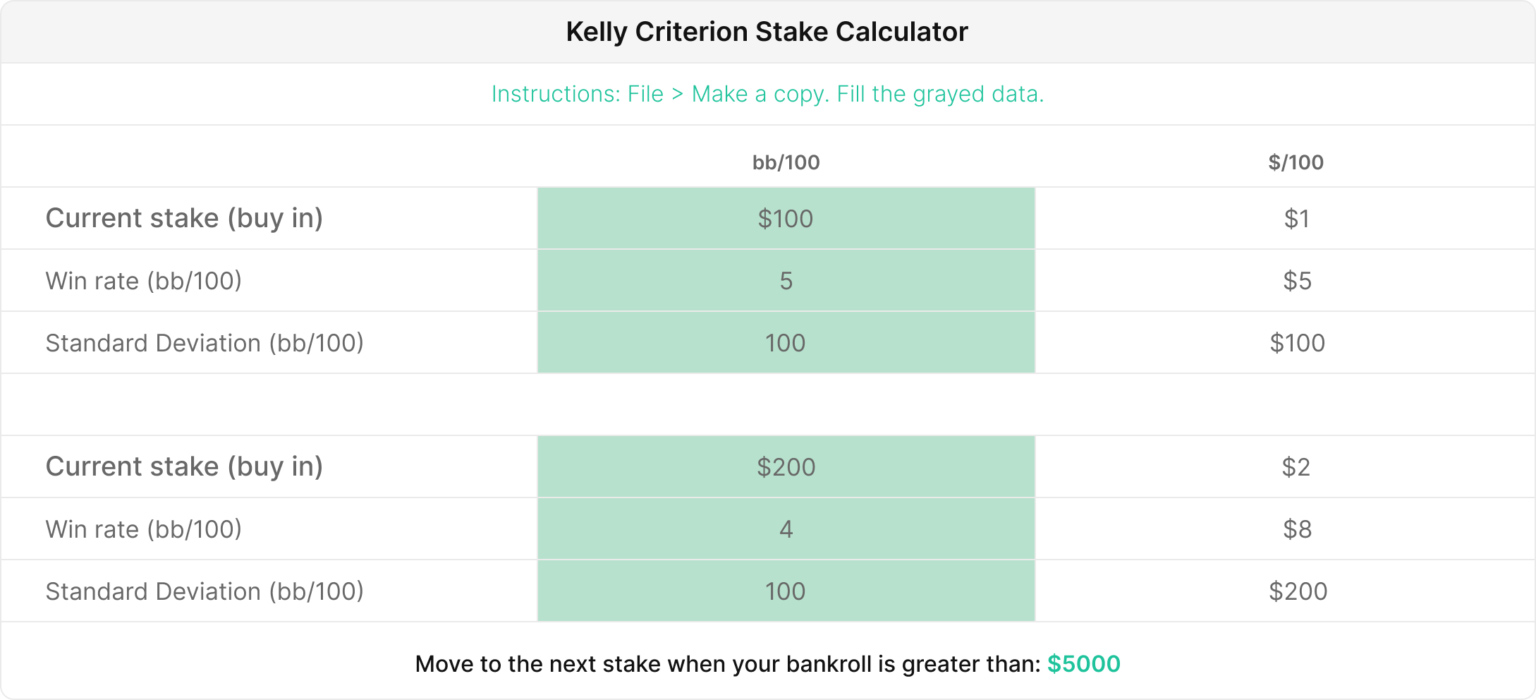
我们还为 MTT 玩家提供了(测试版)计算器! 对于具有多种结果(锦标赛排名)的投注,凯利变得更加复杂。 有些结果会导致您的资金发生巨大变化,而其他结果则相当小。
最大化此方程以找到 MTT 中的最优 BRM 策略:

在哪里
概率代表锦标赛中每个位置的概率。
结果代表您在锦标赛中某些名次的资金变化。 例如,如果排名第一会使您的资金增加 20%,则该结果的分配值为 1.2。 如果失败使您的骰子减少 1%,则该结果的分配值为 0.99。
为事件中每个可能的结果添加一个术语。
在实践中,给这个方程赋值是相当困难的,但我们可以估计给定一些边缘(ROI)的概率。 请注意,100BI 规则对于大多数大型 MTT 来说过于激进!
倾斜
倾斜被定义为由于情绪困扰而不是理性理由而采取次优行动。 许多扑克玩家在下风期时会因为害怕失去更多的钱或希望赢回之前的损失而屈服。
倾斜可能非常危险,因为如上所述,降低获胜率将导致更大的方差。 这成为一个自我实现的预言,并进一步延长了下跌的持续时间。
我们将在后面的文章中讨论更多有关倾斜管理的内容。
结论

如果说研究扑克方差有什么值得借鉴的话,那就是古老的格言“不要用你输不起的钱去博弈”是正确的。
我们希望,随着您对方差的了解越来越多,它将帮助您更好地理解上涨和下跌的暂时性,并在您的扑克之旅中改善您的心理状态。

