隐含赔率是扑克理论中的一个关键指标。您可能听说过这个术语,并且对这个想法有了基本的了解,然而,这个概念在求解器时代已经发生了很大的变化。
隐含赔率是什么?
隐含赔率是你预期在原始权益之上获得的价值。你可以将其视为当你在后续回合中击败对手时预期获得的价值。此概念与“直接底池赔率”形成对比,用于解释为什么某些牌虽然没有足够的原始权益来跟注,但仍然能够有利可图地听牌。
直接赔率与隐含赔率
举个例子。我们在转牌圈面对 10BB 底池大小的下注。我们持有 25% 权益的听牌。我们应该跟注吗?
直接底池赔率计算
直接底池赔率是指您需要获胜才能至少在跟注时保持收支平衡的时间百分比。这假设之后没有钱投入。
- 25% 的时候我们会拿到抽牌并赢得 20BB(底池 + 对手的下注)
- 75% 的情况下我们会错过并损失 10BB(我们的跟注)
跟注预期值 = (25% x 20BB) – (75% x 10BB) = 5 – 7.5 = -2.5BB
显然,这是一个失败的赌注。然而,这种计算的问题在于,它忽略了之后进入底池的资金——这就是隐含赔率的作用所在!
隐含赔率计算
为了证明这个跟注是合理的,我们需要在河牌圈赢一些额外的钱(M)。如果我们输了,我们随时可以弃牌。
- 25% 的时候我们会拿到抽牌并赢得 20BB + M(底池 + 对手的下注 + M)
- 75% 的情况下我们会错过并损失 10BB(我们的跟注)
呼叫的预期值 = (25% x (20+M)) – (75% x 10)
当我们抽到平局时,我们需要额外赢多少钱才能收支平衡?将 EV 设置为零以找到收支平衡点,然后求解 M:
0 = (25% x (20+M)) – (75% x 10)
M = 10
平均而言,我们需要在河牌圈赢得 10BB 以上才能证明跟注是合理的。这相当于在河牌圈下注 ⅓ 底池。因此,如果我们认为在拿到抽牌时至少可以赢得 ⅓ 底池下注,那么这个跟注就是有利可图的!
换句话说,跟注“意味着”它将在河牌圈赢得(至少)额外的 10BB。这就是该术语名称的由来。
与权益实现的关系
SB 开牌,BB 跟注。翻牌是J♥ T♦ 6♥ 2♣。SB 下注 75%,BB 跟注。SB 转牌超额下注 175% 底池,BB 用 5h3h 跟注。
让我们从一个简单的底池赔率计算开始。我们 (BB) 面临 26.25BB 的下注,底池是 15BB。要通过跟注实现收支平衡,从长远来看我们需要至少赢得 26.25BB。
假设我们持有5♥3♥这样的边际组合抽牌,其权益只有 31.68%。
让我们看看我们的直接底池赔率。所需权益 =(跟注金额)/(跟注后底池 – 佣金)。BB 需要 26.25 / (15 + 26.25*2 – 0.6) = 39.24% 的权益才能跟注。
如果 SB 全押(或者如果河牌总是被看完),这将是一个轻松的弃牌。但是,跟注后仍落后 66.25BB。5h3h 预计在获得抽牌时会赢得比其应得份额更多的权益,因为隐含赔率。
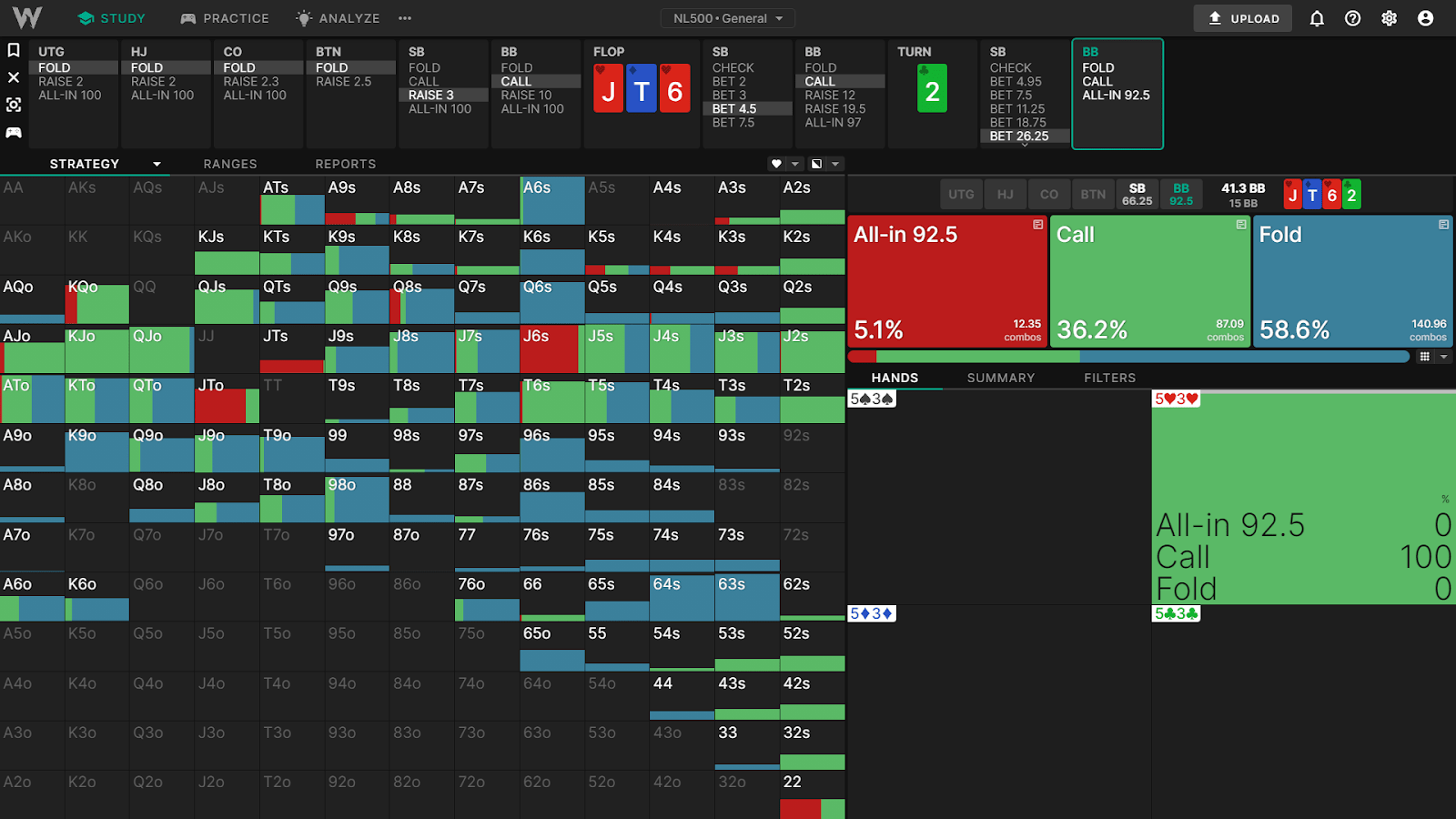
我们的 5h3h EV 比弃牌高 5.33BB。这实际上意味着,我们预计跟注后会赢 (26.25BB + 5.33BB = 31.58BB)。我们跟注后底池将为 67.5BB,因此我们的预期
底池份额为 (31.58 / 67.5) = 46.78% 底池(忽略佣金)。


让我们回顾一下:
- 我们的原始权益为 31.68%
- 我们的底池份额是46.78%
换句话说,我们超额实现了我们的权益:46.78/31.68 = 148%
更准确地说,我们的预期价值高于我们的原始权益所暗示的,因为我们有能力在之后获得更大的价值。这是隐含赔率的基本性质。
反向隐含赔率
反向隐含赔率也存在。例如,有时你会抽到抽牌,但还是输掉一大笔底池。有时一手成牌会因为在后面几轮被压制或抽牌而无法赢得应得的底池份额。拿到第二好的强牌会严重削减你的利润率。
我们回到最初的J♥ T♦ 6♥ 2♣示例,假设我们持有K♠J♠。


K♠J♠ 的胜率很高,领先于对手一半以上的范围。然而,在对手的过度下注面前,它仅能勉强维持收支平衡。当你的对手处于两极化状态时,你的边缘成手牌很难战胜对手的价值牌。这些牌更接近于抓诈唬牌,反向隐含赔率很低。
再次,我们需要赢得 26.25BB 才能收支平衡,而K♠J♠赢得 26.25 + 2.21 = 28.46BB,或大约 28.46/67.5 = 42% 的底池。
原始股权:54.71%
EV:42.16%
股权实现率 = 77%。
换句话说,我们仅实现了 77% 的原始权益。
那么我们剩余的 EV 去哪了?好吧,SB 有能力超额实现他们的权益,并在河牌圈的许多无关紧要的位置放置我们的顶对。他们可以用更强的价值/诈唬来对付我们,超越我们,并堆叠我们的顶对以获得巨额利润。我们无法跟注每个河牌圈的下注。我们有一个诈唬者,因为他们的范围非常强,所以无法从更差的牌中获取价值。
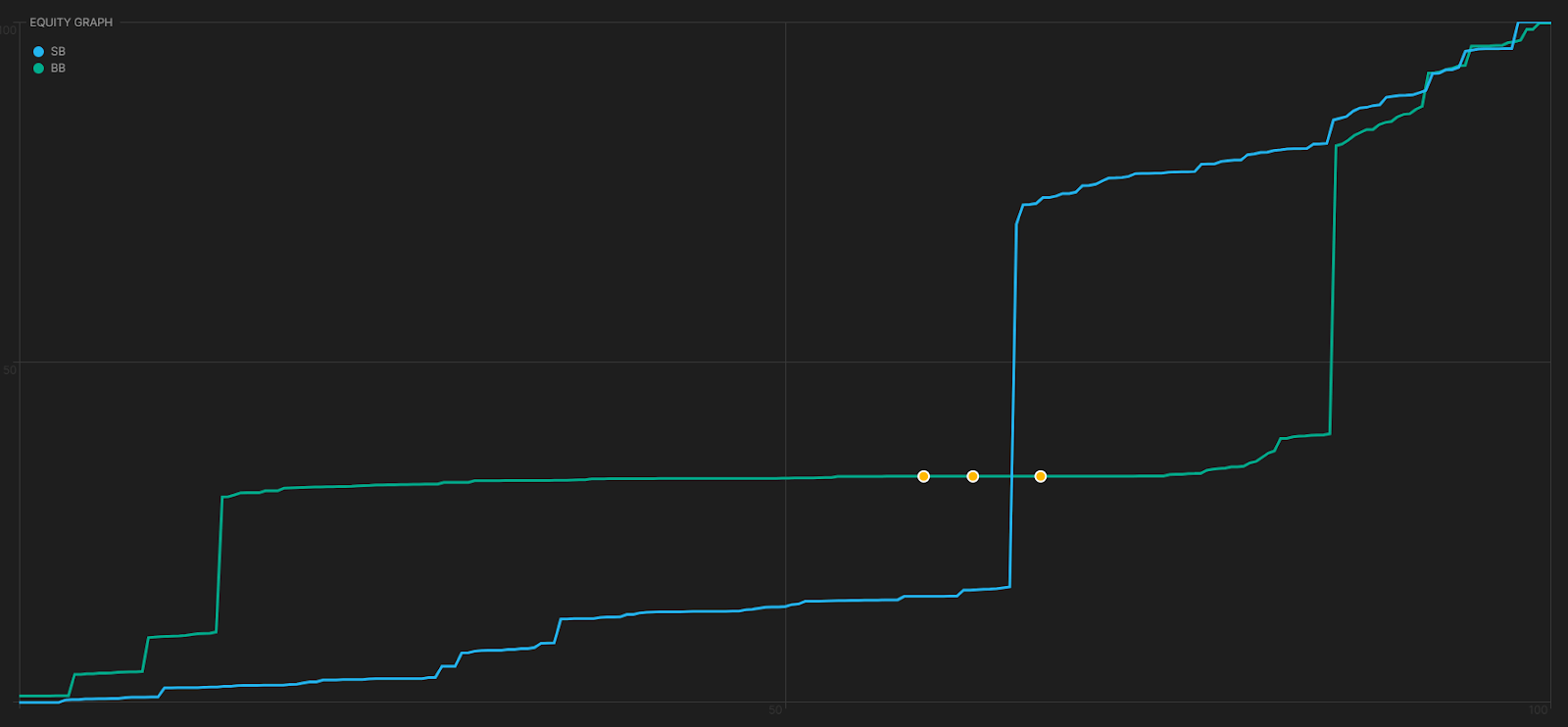
让我们想象一下。这是我们面对他们的过度下注时的权益分布。线上的点代表我们所有的 KJ。正如您所看到的,BB 的范围大部分都无所谓,从那条长长的扁平的 bluff-catcher 线可以看出。
隐含赔率与筹码深度有何关系
筹码深度是评估隐含赔率的最大因素。请记住,“隐含”表示我们期望在后面的回合赢得更多筹码。我们拥有的筹码越多,在后面的回合赢得(或输掉)筹码的可能性就越大,隐含/反向隐含赔率就越高。
让我们比较一下在标准现金游戏中,求解器如何在不同的筹码深度下开出 HJ:
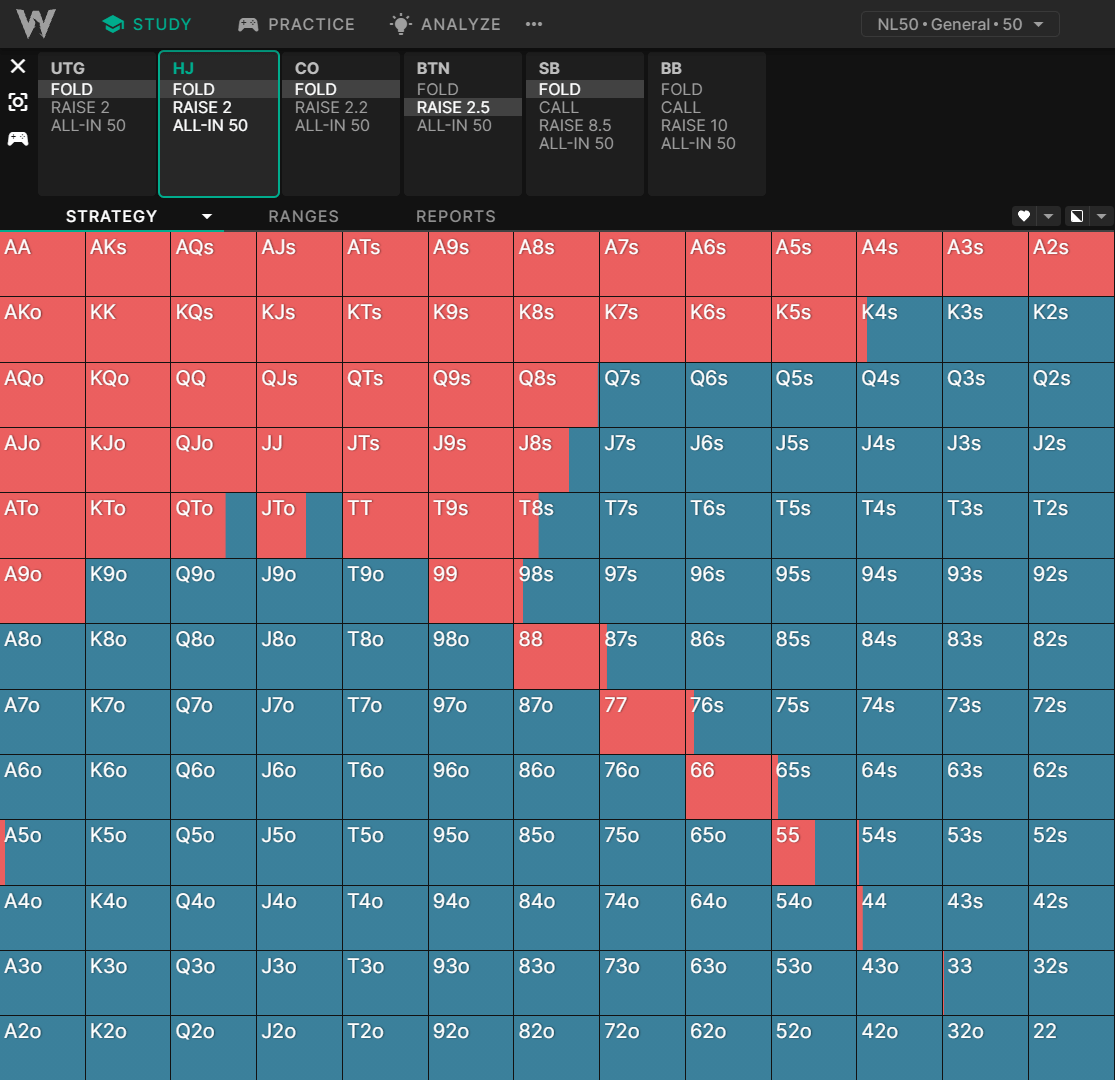
HJ 开局:50BB 深
你还应该考虑对手在后面几轮投入筹码的可能性。例如,如果你的同花听牌在所有同花完成的牌面都失败,那么你的同花听牌的隐含赔率就会较低。
HJ 开局:100BB 深
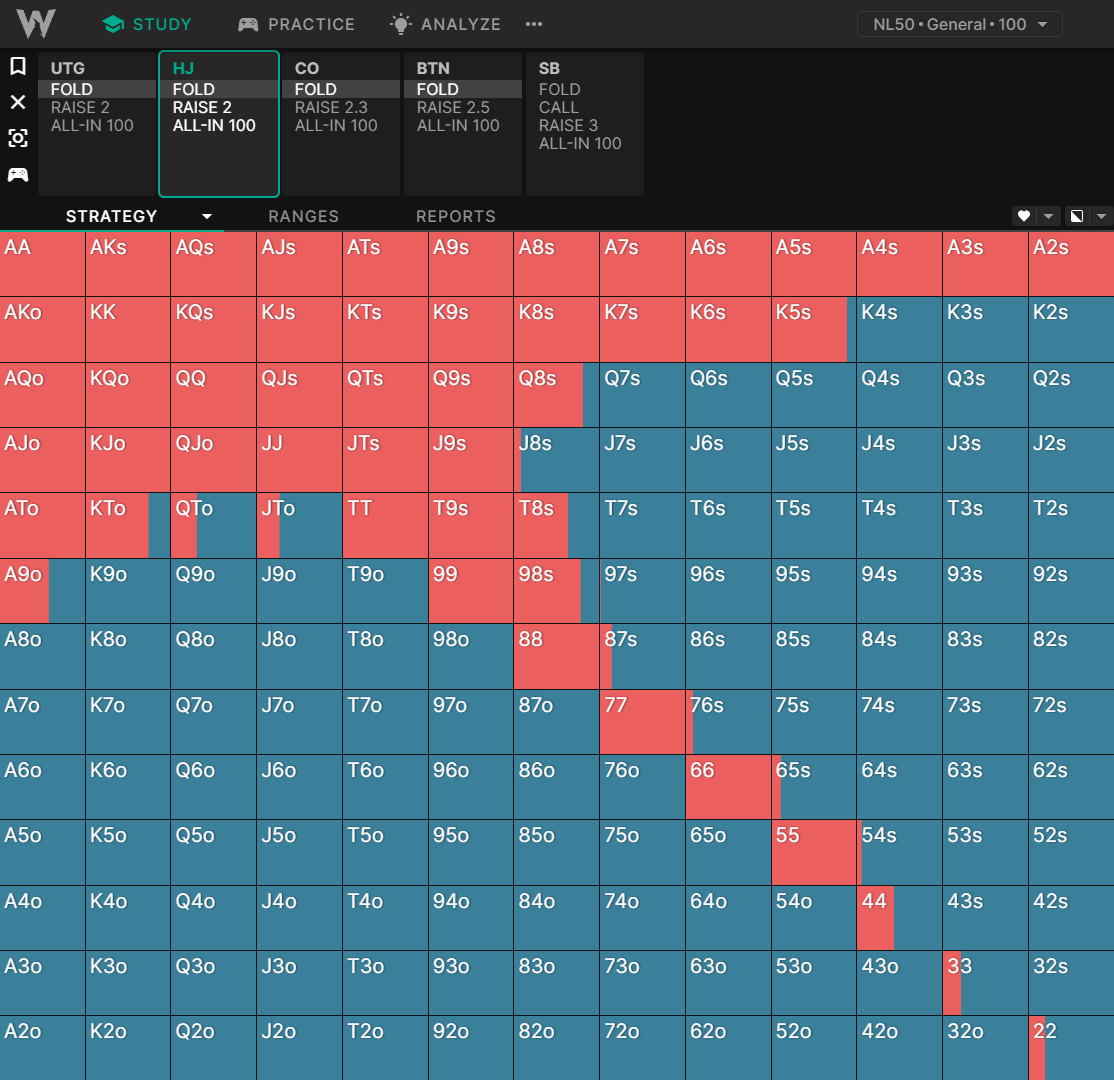
随着我们进一步深入研究,我们发现玩家更倾向于选择低口袋对子、同花连牌以及具有更好隐含赔率的牌。这种影响很微妙,但在锦标赛图表中更为明显:
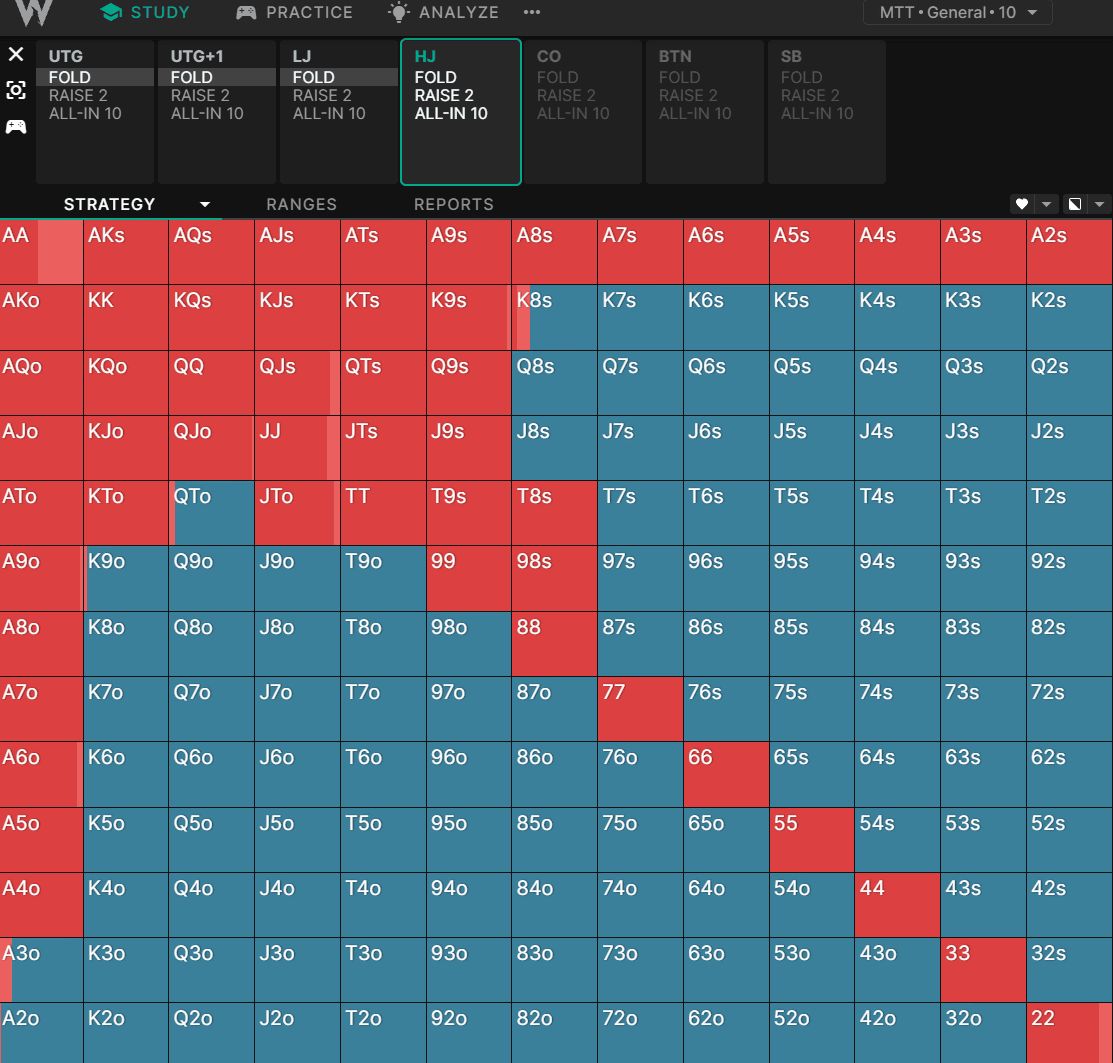
我们可以看到范围从低筹码深度的高胜率全押扩大到更深筹码深度的隐含赔率更高的“可玩”牌。范围在 60BB+ 时缩小,因为其他玩家可以因隐含赔率提高而以更宽的范围进入底池。
通过多向权益保留可视化隐含赔率
隐含赔率与一手牌能否抽到坚果牌有关。我们有时将这种效果称为“可玩性”。以下 gif 是 2-14 名玩家持有任意两张牌时的颜色编码权益分布。在这里我们可以看到权益如何向多方向演变。
注意梯度而不是确切的数字。
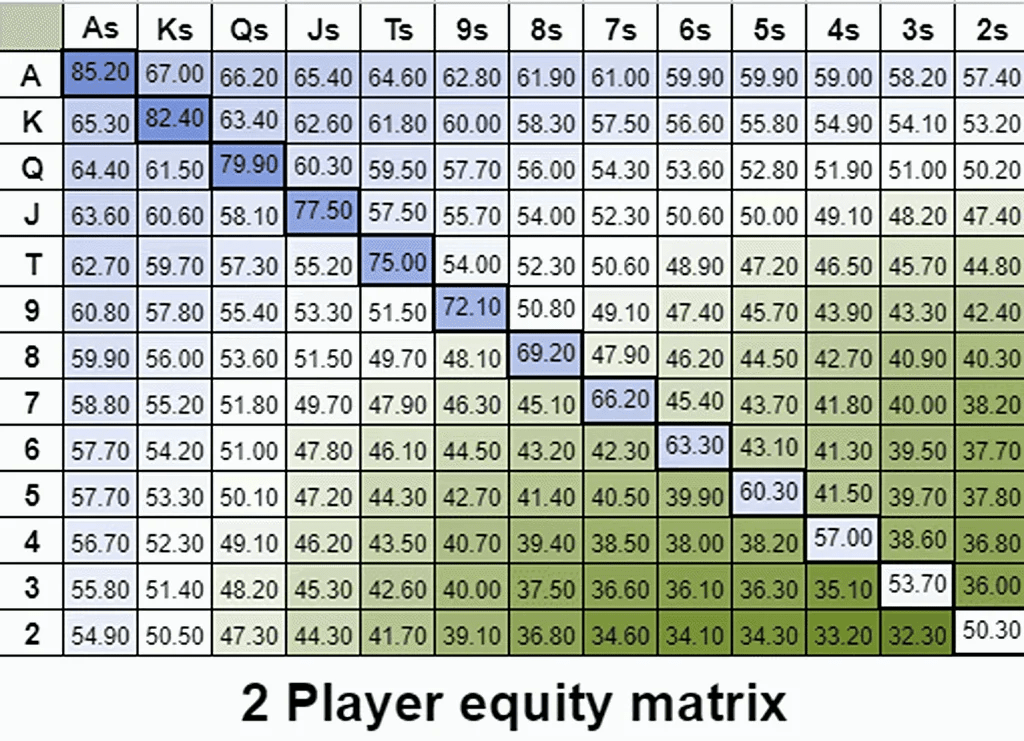
令我惊讶的是,我发现通过调整玩家数量(调整隐含赔率的值),你可以创建与 GTO 开局范围大致相似的权益梯度。例如,这是前 44% 手牌的权益梯度,旁边是标准的 100BB BTN 开局范围。

即使牌局中只剩下 3 名玩家,隐含赔率的价值也会被夸大到 100BB 深。为了复制 GTO EV 梯度,我通过将多路权益计算增加到 8 名玩家来人为地提高隐含赔率。
随着玩家数量的增加,权益梯度会向着更适合且更紧密相连的牌方向转变,这些牌更有可能抽到坚果牌。
通过这种方式,我们将隐含赔率视为一个可调整的参数,以人为地突出不同类型牌的内在隐含赔率(或者更准确地说,一手牌吸引强牌的固有能力)。

即使牌局中只剩下 3 名玩家,隐含赔率的价值也会被夸大到 100BB 深。为了复制 GTO EV 梯度,我通过将多路权益计算增加到 8 名玩家来人为地提高隐含赔率。这种分析低估了阻断效应,这使得复制早期位置的开局范围变得更加困难。无论如何,我希望你喜欢这种隐含赔率的视觉表示,就像我喜欢创建它一样!